알고리즘을 풀면서 문제를 초기에 구상을 했을 때는, 더 빠른 방법이지 않을까 생각했는데, 직접해보니 오히려 추가 작업만 늘어나게 되었던 경우를 포스팅하려고 합니다.
// https://school.programmers.co.kr/learn/courses/30/lessons/87389
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
위 문제는 나머지가 1이 되는 수를 찾는 문제입니다.
초기 구상 단계
1. 나머지가 1이되는 최소의 수를 구하는 것이기에, 차라리 n-1이 소수인지만 확인
2. 그렇지 않다면 해당 수를 반환 .. 해당 수의 약수가 존재한다면 최소공약수를 반환
3. 범위는 타겟의 제곱근까지만 확인( 그 이상은 확인할 필요가 없으므로)
이라고 생각했다. 그렇기에 소수를 구하는 에란토스체를 사용하면 런타임을 최소화 할 수 있지 않을까 생각했습니다.
우선 간단하게 타겟 수의 제곱근보다 작은수들로 n-1을 나누어 보았습니다.
function solution2(n) {
const min = n - 1;
for (let i = 2; i < Math.sqrt(n); i++) {
if (min % i === 0) {
return i;
}
}
return min;
}
이후 이전에 학습했던 에란토스체를 사용해서 나누어 보았습니다.
function solution2(n) {
const min = n - 1;
const prime = new Array(n + 1).fill(1);
for (let i = 2; i < Math.sqrt(n); i++) {
if (prime[i]) {
if (min % i === 0) {
return i;
}
// 배수값들 거르는 작업
for (let j = i ** 2; j <= n; j += i) {
if (prime[j]) prime[j] = 0;
}
}
}
return min;
}
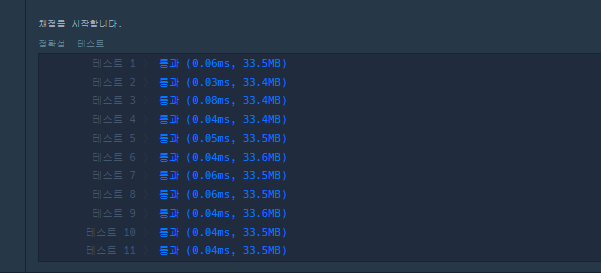
오히려 더 느려졌네요.. 왜 그럴까요? 에란토스체를 소수를 판별하는 가장 빠른 방법인데?
결론부터 말하면 부가적인 작업이 오히려 많이 생겼기 떄문입니다.
문제의 목적은 사실 n-1의 최소공약수를 구하는 문제입니다. n의 제곱근보다 작은 모든 소수를 구한 다음에 나눌 필요가 없는거죠.
소수를 구하는 단계에서는 각각의 수가 소수인지 일일이 확인하는 것보다, 미리 소수의 배수들을 제외시키면 소수인지 판별하기 훨신 쉽습니다.
하지만 이 경우 n-1이 소수인지만 판별하면 되는데, 부가적인 작업이 오히려 더 많이 생긴 것 입니다.
그렇기에 오히려 간단한 첫 번쨰 코드의 성능이 가장 좋았던 것이죠.
추가적으로 위 코드에서는 Math.sqrt의 계산을 반복문 내에서 수행할 필요 없이, 반복문 밖에서 한 번만 계산하도록 최적화 할 수 있습니다.
function solution3(n) {
const min = n - 1;
const prime = new Array(n + 1).fill(1);
const limit = Math.sqrt(n);
for (let i = 2; i < limit; i++) {
if (prime[i]) {
if (min % i === 0) {
return i;
}
// 배수값들 거르는 작업
for (let j = i ** 2; j <= n; j += i) {
if (prime[j]) prime[j] = 0;
}
}
}
return min;
}
따라서 첫 번째 정답도 가장 최적화를 한다면 아래 코드가 됩니다.
function solution(n) {
const min = n - 1;
const limit = Math.sqrt(n);
for (let i = 2; i <limit; i++) {
if (min % i === 0) {
return i;
}
}
return min;
}
'알고리즘 문제풀이' 카테고리의 다른 글
| 9466 텀 프로젝트 (Node.js) (0) | 2023.11.17 |
|---|---|
| 백준 2842 집배원 한상덕 코드 리뷰 (node.js) (0) | 2023.11.08 |
| Node.js) 백분 1016 제곱 ㄴㄴ 수 (1) | 2023.10.30 |
| 카카오 신고결과 받기 문제 - ( 프로그래머스) (0) | 2023.09.10 |
| 소수찾기(에라토네스 체) 프로그래머스 (0) | 2023.07.11 |