문제링크 : https://school.programmers.co.kr/learn/courses/30/lessons/64062
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제를 풀었는데, 내 방법은 13번에서 효율성에 통과하지 못했다. 하지만 해당 원인에 대해서 처음엔 잘 이해하지 못했고, 다른 사람의 풀이를 보고 고민한 결과를 정리하고자 게시글을 작성하게 되었다.


문제는 위와 같다.
요약하자면 현재 돌 보다 밟을 수 있는 횟수가 작은 돌이 연속으로 k번 이상 나오게 되면 건널 수가 없다.
나는 위와 똑같은 논리를 코드로 구현하고자 하였다.
function solution(stones, k) {
// 돌의 갯수
const arrayLength = stones.length;
// 한번에 건널 수 있는 수와 돌 수가 같다면 최대값이 답.
if (arrayLength == k) {
return Math.max(...stones);
}
// 초기에는 k번쨰 수중 가장 큰 값이 최대값
let answer = stones[0];
for (let i = 1; i < k; i++) {
if (stones[i] > answer) {
answer = stones[i];
}
}
// 이후 반복문을 통해서, 다음번의 돌들이 연속으로 k번 작을 경우 answer를 교체
for (let i = 0; i < arrayLength - k; i++) {
let max = 0;
const current = stones[i];
let flag = false;
for (let j = 1; j <= k; j++) {
if (current < stones[i + j]) {
flag = true;
break;
}
max = Math.max(max, stones[i + j]);
}
if (!flag) {
answer = Math.min(answer, max);
}
}
return answer;
}
로직에 문제가 없다면 정확성에선 통과하지만, 효율성에서 13번에서 걸리고 말았다.
이 당시에는 왜 13번만 통과를 못하지에 대한 해답을 찾지 못하였고, 나와 같은 문제를 겪은 사람이 있을까 질문하기에 들어갔다.

그 결과 대부분을 이분탐색을 통해서 문제를 푼다는 것을 알게 되었고, 이를 참고하여서
function solution(stones, k) {
//이분 탐색 좌우
let left = 1;
let right = 200000000;
while (left <= right) {
const mid = ((left + right) / 2) >> 0;
let count = 0;
// 반복문을 통해서 연속으로 k번 나오면 break, 이후 정답에 가까운 값을 다시 탐색)
for (let i = 0; i < stones.length; i++) {
if (stones[i] - mid <= 0) count++;
else count = 0;
if (count === k) break;
}
// 만약 연속 k번 나오면 right를 교체(현재 값이 최댓값을 넘었다)
if (count === k) right = mid - 1;
// 아니라면 더 큰 값이 있는지 찾기 위해서 left를 교체
else left = mid + 1;
}
return left;
}
위 방법은 내 방법과 다르다.
내 방법은 각각의 숫자를 비교하면서 일일이 최댓값을 교체해주는 방식이면, 이분탐색 방법은 정답을 임의의 값으로 정해놓고 비교한 후 정답을 수정하는 방식이다. (200000000가지 중에서 이분 탐색을 통해서 정답을 찾는 방식)
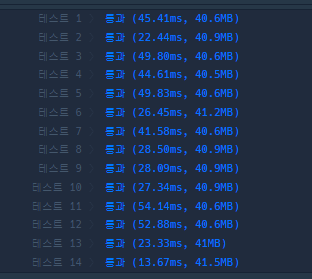
내 방법과 다르게 대부분의 방식에선 속도가 느린데, 13번만 유독 빠르다.
이에 대한 호기심을 해결하기 위해서 두 방식의 시간 복잡도를 계산해 보려고 하였다.
내 방법의 시간복잡도는 n * k 이다. ( n: 배열의 길이 , k : k의 값)
k가 길어질수록 반복 계산이 많아진다.
정답에 통과한 두 번쨰 방법의 시간 복잡도는 nlogM이다( n: 배열의 길이, M은 left와 right의 간격 200000000)
이분 탐색을 통해 찾기 때문에 만약 정답이 중앙에 가까울수록 속도가 빠를 것이다.
즉 테스트에서 대부분 내 값이 빨랐던 이유는 k 값이 log( 200000000)에 비해서 작았기 떄문이다.
하지만 가장 오래 걸리는 값을 기준으로 했을 때는 후자가 훨씬 좋은 방법이다.
회고
문제를 풀면서, 시간 복잡도에 대해서 깊게 생각하지 않았기 때문에 좀 더 막막하게 느껴졌었던 것 같다.
백준에서 시간 복잡도의 중요성을 느끼지만, 막상 문제 풀 때는 문제 유형에 맞춘 방법을 사용했었다... 안 좋은 습관인 거 같다. 막상 혼자 밑 바닥 부터 생각해야 할 때, 좋은 방법이 잘 떠오르지 않았느데, 이번 기회에 시간 복잡도와 문제를 고민하는 방법에 대해서 다시 생각하게 되었다.
'알고리즘 문제풀이' 카테고리의 다른 글
| node 1005 ACM Craft 풀이 (0) | 2024.04.13 |
|---|---|
| 자바스크립트 셔틀버스 문제(카카오) (1) | 2024.02.13 |
| 백준 1019 책페이지 (자바스크립트 , Node.js) (3) | 2023.12.04 |
| 백준 1119번 그래프 (Node.js) (0) | 2023.12.04 |
| Node.js 알고리즘에 사용할 우선순위큐 만들기 (0) | 2023.11.24 |